On a Moreau Envelope Wirelength Model for Analytical Global Placement

题外话：Peiyu 这篇文章 Bei Yu 自称是 DAC 2023 最强论文 --> With Yibo Lin --> Moreau Envelope Wirelength Model

References --[zhihu](Design Automation Conference (DAC)2023 现在进展如何? - 知乎)

Introduction

广泛采用的策略是线长驱动的全局布局，使整个电路线长最小化。分析型布局方法讲布局问题表达为一定合法约束的布线问题。

计算能力和神经网络发展，数值优化方法(numerical optimization approaches)得到了极大关注。要求线长模型处处可微(differentiable)。但是由最大最小坐标的 HPWL 半周线长模型不是处处可微分的。所以，当代布局算法严重依赖于可微分的 HPWL 模型。主要有两种区别 --> 二次近似(quadratic approximations)和非线性近似(nonlinear approximations)。

二次近似模型：用平方长度近似每个边的成本，给出了一个严格凸的目标，方便我们优化。二次近似模型一般具有封闭形式的最小值，可通过求解线性系统找到。
- 二次近似模型为了更好近似HPWL参数，提出线性化技术，与某些净长度成反比的权重做积分，使得加权平方项更接近HPWL eg. --> Bound2Bound (B2B) model。eg:

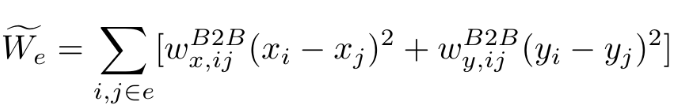
非线性近似模型：通常非线性模型采用可微函数，比如对数、指数(log-sum-exp)，或者加权平均(weighted-average)。通过控制超参数 r 近似 HPWL 任意精度。
- eg. DREAMplace 等采用这种方法。
新的模型：
- eg.Bivariate-Gradient-Based (BiG) model 双变量梯度模型：用近似双变量最大值或者最小值的双变量函数来计算相对于坐标的梯度。提高数值稳定性和 CPU 运行时间。
- eg.Subgradient-based approaches 基于次梯度方法：直接优化 B2B 模型。

Sum up：

WA（weighted average）模型比LSE（log-sum-exp）模型有更低的逼近误差值，但仍然面临数值稳定性和非凸问题。对比之下，BiG模型有数值稳定性和廉价计算优点，但是依赖于指定的双变量线长模型。非光滑优化方(Non-smooth optimization approaches)不需要任何的近似可微，但是可能遇到收敛速度慢和收敛性差问题。

我们提出一种新的可微线长模型，使用 Moreau envelope 来近似HPWL。该模型在数值稳定性，凸性和逼近误差方面都好于以往模型。

贡献如下：

推导了非光滑HPWL函数的近似算子(proximal mapping)显式表示。提出了类似通信系统的注水算法解决近似算子(proximal mapping)和Moreau envelope问题。
提供了理论和实验分析，比较以往算法，验证可行性。
实验表明，提出模型可实现在ISPD06数据高达5.4%的HPWL改进，ISPD06竞赛benchmark超过1%；ISPD19数据高达3.0%的HPWL改进，ISPD19竞赛benchmark超过1.5%。

Preliminaries

Analytical Global Placement（分析全局布局）

电路布局一般包括三部分，global placement（全局布局），legalization（合法化），detailed placement（详细布局）。在全局布局 GP 阶段，目标找到总线长最小的放置位置，并且重叠控制在最低水平，典型的非线性全局布局表示为：

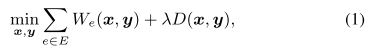
HPWL 模型定义为 We,表示为：

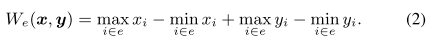
定义 HPWL 函数是凸和连续，但不是处处可微。

Nonlinear Differentiable Models（非线性微分模型）

log-sum-exp (LSE) model

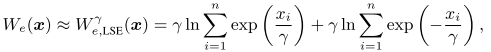
weighted average (WA) model

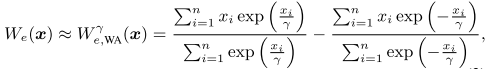
参数 r 是控制精度和可微性权衡的超参数。r --> 0+ ，近似任意接近于真实的 HPWL。通常在全局布局 GP 早期阶段，r 设置成一个比较大的值，使得目标变得平滑，随着迭代 step 增多而减小。

Moreau Envelope

（os：此处需要凸优化数学基础）

一般的Moreau Envelope定义满足真实Hilbert空间上特定约束的函数。在布局应用中，我们只需考虑定义Rn中下界闭凸函数h(x):

Any t > 0，

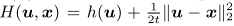
其中Moreau Envelope的ht定义为：

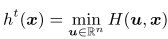
不要求ht为光滑函数。

近似算子定义为：

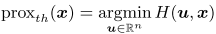
由上公式得，Moreau Envelope的ht是自然可微，梯度是全局Lipschitz连续的。envelope theorem指出：

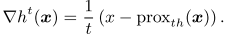
Since

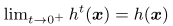
t被认为是近似精度，类似LSE和WA中的r。

在全局布线中，HPWL 中的 We 是一个干净直接公式。我们提出一种算法计算 Moreau Envelope 中的 We，使用 We + t 作为近似线长模型，使整个目标处处可微。

Comparison between WA and the Moreau Envelope models（对比）

比较 WA 和 Moreau Envelope 模型。

Numerical Stability（数值稳定性）

指数项对 x 坐标敏感，小的 r 导致数值溢出，LSE 和 WA 模型都必须面对这样问题。

Non-Convexity（非凸性）

没有理论和实验保证 WA 模型凸性。以一个 3pin 网表为例，水平轴（横轴）代表 pin 坐标，调整 r 参数绘制函数曲线。eg.图 1(a):

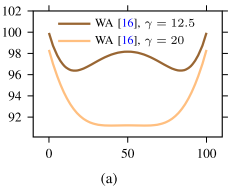
验证在不同 r 下，WA 模型函数凹凸性难保证。

Approximation Error（近似误差）

线长模型可能是高维，比较难分析。因此对平滑参数 r 和 t 进行实验。给定 X = Xmax - Xmin = 200，随机生成 3000 次不同平滑参数的水平坐标 x ，使用不同线长模型计算近似 x，取平均值。eg.图 1(b):

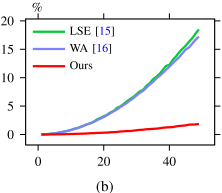
我们提出的模型在近似误差上取得了较好的效果。但是并不是说较低的近似误差就意味着更好的放置质量，这是个比较复杂的因素。除了误差，还有梯度也应该仔细考虑，详细见第四节。

Algorithm

采用 Moreau Envelope 模型比作 HPWL 近似可微，使用 Relu 作为激活函数。

The Gradient of the Moreau Envelope（Moreau Envelope 梯度）

HPWL 函数水平部分表示为

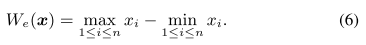
水平和垂直方向都是对称，我们只需要关注水平方向分析。

Theorem 1 定理 1 陈述了近似算子的表示。Corollary 1 推论 1 推广了定理 1，告诉我们如何在给定参数 τ1 和 τ2 情况下计算梯度。

Theorem 1

Corollary 1

Water-filling Algorithm（注水算法）

（os：参考通信信道中关于注水算法解释

公式 7 和公式 8 给了近似算子的显示表示，其中 τ1 和 τ2 不以封闭形式表示。所以需要先求出公式 8 中方程，获得 proxWe 的精确值。

以 τ1 为例子，我们要求解方程：

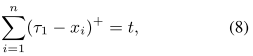
假设有一个 4 pin 的网络，引脚坐标为 X1、X2、X3、X4，eg.图 2(a)：

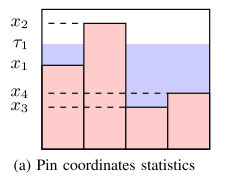
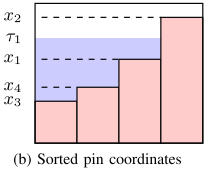
我们需要找到一个 τ1 值，使得蓝色面积为 t。–> 获得 τ1 值的过程 --> 通信中的 Water-filling 注水算法。eg.图 2(b)：

eg.算法 2：

Water-filling 算法是一个直观且高效的方法，解决近似算子中参数 τ1 和 τ2 计算问题，通过对引脚坐标进行排序，这个算法可以迅速地确定所需的参数，进而允许优化算法继续进行。

Nonlinear Optimization（非线性优化）

r 在 WA 方法和 t 在我们方法对解的质量是重要的。

eg.ePlace 方法中使用溢出(overflow)ϕ 来更新参数 r：

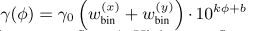
更高的溢出 ϕ 需要更大的 r 牺牲精度来保证可微性。为了更好适应线长模型，使用基于切线的更新方法：

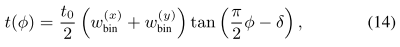
t0是初始值 --> fix t0 = 4
ϕ是密度溢出
w(x)是水平bin大小
w(y)是垂直bin大小
δ是很小正数 --> 避免数值溢出 --> fix δ = 0.0001

对于起初的全局布局表示:

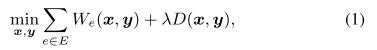
我们遵循 DREAMPlace3.0 和 elfPlace 中温和方案来迭代更新上述方程中的权重密度 λ：

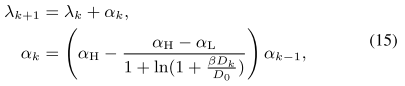
Dk表示第k次迭代的密度
αH ≥ αL > 1 表示密度权重增加速度 --> fix (αH , αL) = (1.01 , 1.02)
β = 2000

Wirelength Model Analysis

Approximation Bound（近似界）

Theorem 2

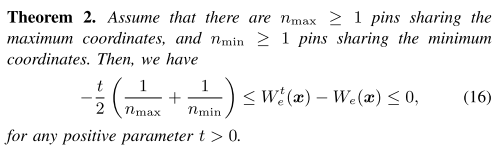
描述 Moreau Envelope 函数如何逼近原始函数，与 LSE 和 WA 类似，这里使用的 Moreau Envelope 也可以任意精度近似 HPWL，证明未给出。

Gradient Properties（梯度属性）

理想情况下，平滑参数趋于 0，任何可微分模型梯度都应趋于 We。

Theorem 3

Theorem 4

Theorem 5

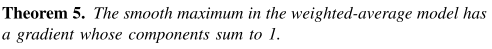
Corollary 2

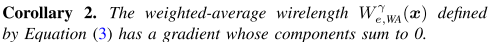
Theorem 6

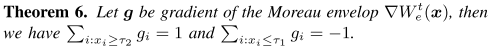
Corollary 3

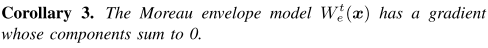
Result

Benchmark

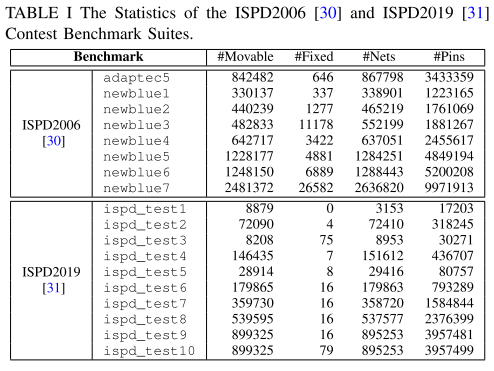
ISPD 2006 、ISPD 2019，eg.表 1：

Base on CUDA/C++ --> DREAMPlace

CPU: Intel Xeon 2.90GHz CPUs ; GPU: NVIDIA GeForce RTX 3090 GPU

HPWL & Runtime in ISPD 2006 and ISPD 2019

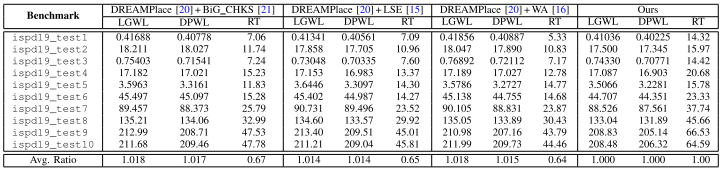
表格 II 显示了在 ISPD2006 基准测试后详细放置的线长改进超过 1%，特别是在具有大量可移动宏的 newblue1 上改进超过了 5%。

表格 III 显示了在最新的 ISPD2019 基准测试上的线长改进超过了 1.5% 到接近 2%。

Wirelength during Global placement（线长趋势）–> Ablation Study（消融实验）

选用 ISPD06 中 newblue1 & ISPD2019 中 ispd19_test10。

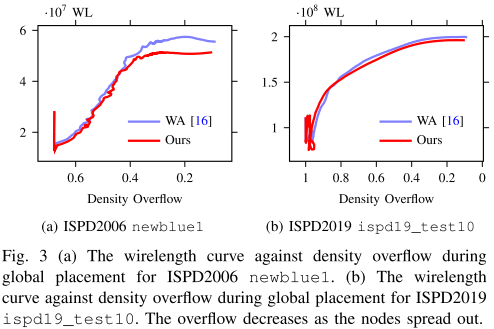
与 WA 相比，在详细放置后，我们可以分别实现约 5.4% 和 1.6% 的改善。

我们的模型获得的线长结果在相同密度溢出时更好。(密度溢出大致反映了整个单元格重叠) --> 相同的密度溢出下，较小的线长意味着更好的布局质量。