Versatile Multi-stage Graph Neural Network for Circuit Representation
本篇文章来自北大 Guojie Song 组和华为 Noah 发布在 2022 NIPS 上的文章。
paper
code
Introduction
EDA 包括不同阶段的电路设计,特别是逻辑综合阶段(logic synthesis stage)和布局阶段(placement stage),如图 1 所示:
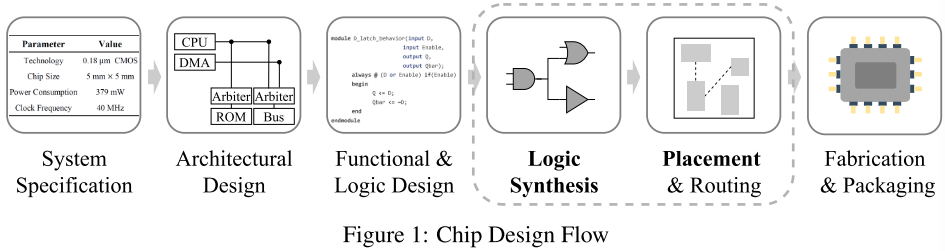
研究人员使用 DL 技术复制电路设计。在芯片设计早期阶段,在预测电路质量和实用性方面取得进展,加快优化速度,减少优化成本。e.g. 在物理设计阶段对电路进行拥塞(Congestion)预测,帮助检测电路缺陷,避免生产有缺陷芯片;在逻辑综合阶段预测,进一步节省芯片设计成本。
电路设计过程复杂性,遇到各种不同设计阶段信息源。其中逻辑综合和布局决定电路质量。如图 2:
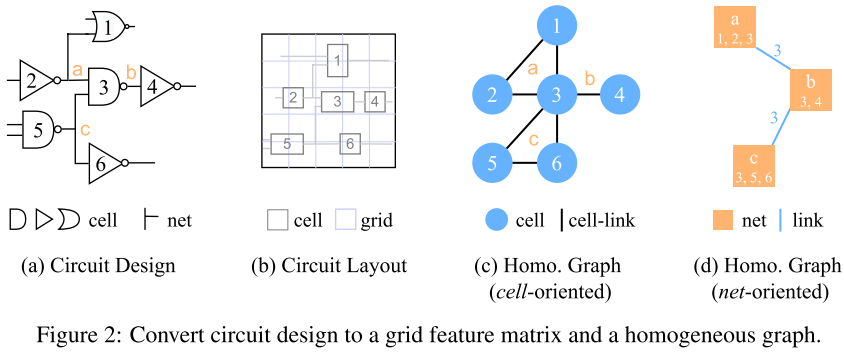
在逻辑综合阶段,电路设计被表示为 Netlist(网表)–由 cell 和 nets 组成。其中 cells 指单元, nets 指连接 cells 的超边(i.e. hyper-edges)。
在布局阶段,获得一个拥有单元位置的版图。此外,下游任务可能需要学习 cells 和 nets 表示。所以更好组织和融合电路表示是一个重要研究问题。
信息可分为 geometrical information(几何信息)和 topological information(拓扑信息):
-
**geometrical information(几何信息):**标准单元(standard cells的位置)
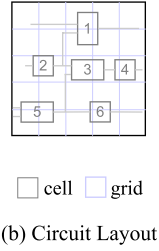
*geometrical method(几何法)*几何模型将电路设计转化为网格特征矩阵(grid feature matrices,比如图2.b),使用cv技术预测性能。
-
**topological information(拓扑信息):**Netlist(网表)只包含拓扑信息(e.g. Cell 类型和cells与nets之间的逻辑关系)
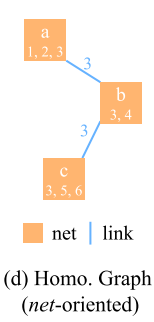
*topological method(拓扑法)*将电路设计转化为 homogeneous graphs(同构图,比如图2.c,d),使用GNN解决问题。
拓扑方法只考虑网表中拓扑信息,不能有效感知布局后引入的几何结构,抑制布局后性能。几何模型严重依赖几何信息,忽略网表拓扑结构,不能再没有几何信息情况下对电路进行全局布局之前阶段处理。只要在逻辑综合阶段或者布局阶段电路上工作良好,两者都不兼容。本文提出需求:
-
设计一种即适用于逻辑综合阶段又适用于布局阶段的数据结构;
-
提出一种兼容两个阶段和各种下游任务的高效有效电路表示模型。
本文首先将电路设计转化为电路图(Circuit Graph ,见图 3),这是一个保留大部分拓扑和几何信息的异构图。一个电路网络包括两种类型顶点:cells and nets。使用连接 cells 和 nets 的引脚(pins)来表示拓扑,称为拓扑边(topo-edges)。在布局阶段处理电路时,额外连接几何上比较接近的 cells,称为几何边(geom-edges)来表示几何。
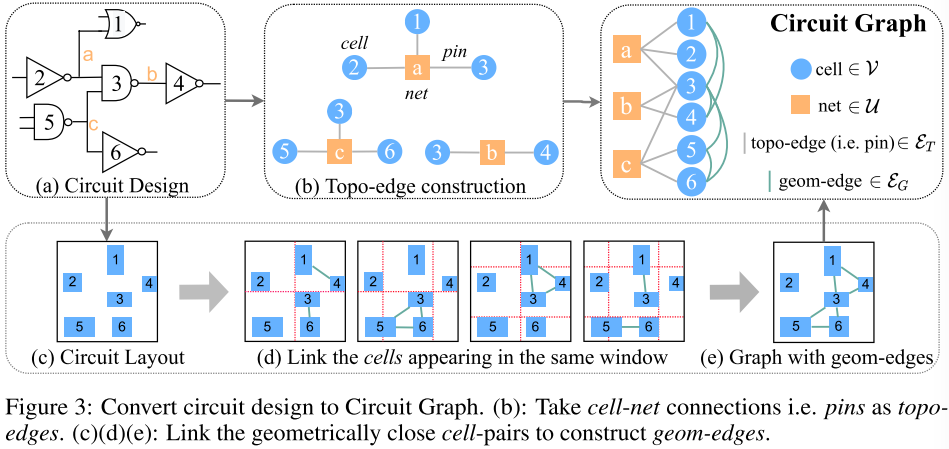
本文设计电路 GNN,为了收集和丰富拓扑和几何信息,提出拓扑边(topo-edges)和几何边(geom-edges)进行信息传递,将信息融合更新单元和网络表示。进一步挖掘拓扑和几何之间深层关系。总结贡献有 3 点:
-
本文提出一种新的信息集成方法—— **Circuit Graph **,将拓扑信息和几何信息结合在一起异构图,能在 cells,nets 或者其他阶段处理不同任务。这是第一种将 EDA 任务和阶段统一兼容的表示方法。
-
本文提出一种新的消息传递范式(message-passing paradigm)—— **Circuit GNN **,在拓扑边和几何边上分别传递信息,对消息进行融合更新 cells and nets 表示。本文设计的效率和有效性在证明和实验上都得到了验证。
-
实验证明在 **Circuit Graph **多阶段/多任务上的优越性能和效率。对于逻辑综合接单的电路拥塞预测任务,与 SOTA 模型相比,其平均网格准确率提高了 16.7%。在布局阶段,拥塞预测任务的精度提高 5.6%,速度提高 10 倍,线长预测任务误差提高 16.9%。
Related Work
Topological Methods
EDA 中拓扑学方法侧重于 cell 和 net 之间的逻辑关系,通常将电路设计重构为有顶点(vertices)和边(edges)的图。CongestionNet 中解决方案将通过网络连接的 cell 链接起来,如图 2.c,并采用流行 GNN 用于拥塞预测。
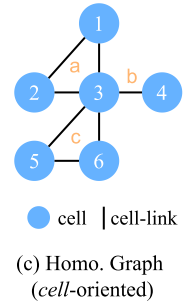
为了处理 net 长度识别和 net 延迟预测,Net2 将连接一个 cell 的 net 链接起来,如图 2.d,并制定 GNN 获得网络表示。
Geometrical Methods
EDA 中几何方法侧重于电路设计中的空间信息。一种通用的方法是将电路分割成小矩阵,i.e. grids(网格),并转化为 RGB 通道。其中 grids 视为像素。然后将网表结构和电路特征编码到绿色和蓝色通道中,红色通道则留作预测目标(e.g. 拥塞)。最后用图像翻译(e.g. pix2pix)方法输出到红色通道中填充新图像,间接解决 EDA 任务。
然而前沿的 LHNN 并没有将电路转化为图像,而是转化为晶格网络(lattice networks),每个 grids 作为 network 中内部 node,并且每个 net 作为外部 node 被几何连接到覆盖的 grids。LHNN 成功使用几何方法增强拓扑信息,实现 SOTA 性能,但只能处理拥塞预测任务,并且只能处理有布局信息的电路。
(os:文中提及的晶格网络(lattice networks)本人认为假设一个电路被划分成多个小网格,每个网格代表电路的一部分。这些网格之间有些是直接相邻的(形成内部节点),而有些网格之间通过电路连接(形成外部节点)。晶格网络就是将这些网格和连接关系以规则的网络形式表示出来。)
Circuit Graph
Circuit Featurization
电路设计最初设计由
-
表示为 cell 的大小和对 net 的连接度; -
表示为存储 net 的跨图和 cell 的连接度。
除了 cell 和 net 的基本属性之外,拓扑和几何在电路设计中也起重要作用。pins 引脚
几何方法将电路切割成更小的矩阵,即 grids,并通过合成 cells 的
Definition 1(Geometry-driven Circuit Featurization)
$\mathcal{F}{G}={X{gr}}
-
Grid feature
主要包括 pin 密度和 net 密度。由于 结构类似于图像处理 RGB 通道,因此很容易采用 CV 模型(e.g. CNN)处理几何信息。
Definition 2 (Topology-driven Circuit Featurization)
拓扑方法倾向于将电路设计构建成二分图(bipartite graph)def2.
$\mathcal{F}{T}={\mathcal{V},\mathcal{U},\mathcal{P},X{\mathcal{V}},X_{\mathcal{U}},X_{\mathcal{P}}}
-
然而,
通常被简化为同构图(Homogeneous Graph),馈送给一些流行 GNN(e.g. GAT 图 2.c and d),导致了异构信息丢失。
Definition of Circuit Graph
为了更好利用上述两种常用的电路特征,本文提出了一种新的方法,将电路中拓扑信息和几何信息编码到一个统一的异构图(Heterogeneous Graph)中。如图 3 所示:
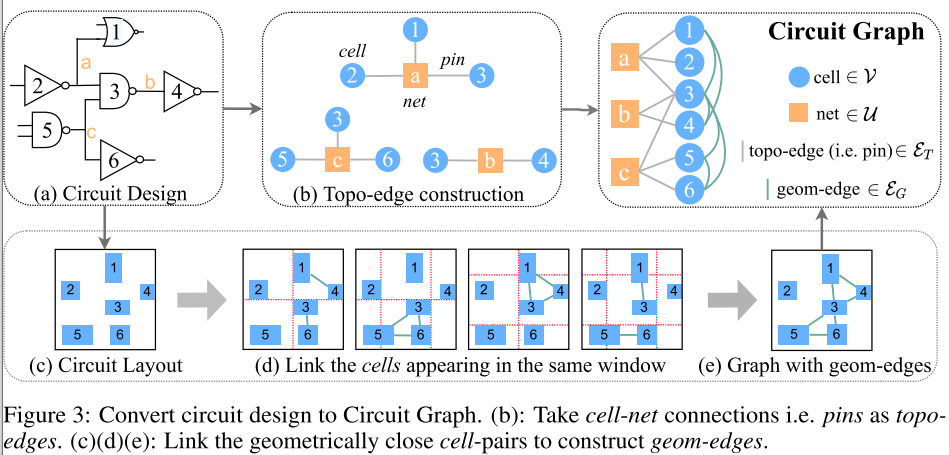
首先将 pins 作为拓扑边(topo-edges)($\mathcal{E}{T}=\mathcal{P}\mathrm{and}X{\mathcal{E}{T}}=X{\mathcal{P}}
Definition 3 (Circuit Graph)
A Circuit Graph $\mathcal{G}={\mathcal{V},\mathcal{U},\mathcal{E}{T},\mathcal{E}{G},X_{\mathcal{V}},X_{\mathcal{U}},X_{\mathcal{E}{T}},X{\mathcal{E}{G}}}
-
为了保留拓扑信息,Circuit Graph 完全继承 def2 中的
及其特征在 ,而不是简化成同构图避免异构信息丢失。 -
对于几何信息,为了避免计算所有
中 cell-pair 的距离,并将时间成本减少到 ,本文通过大小为 的移动窗口将 cell 分开,并将同一窗口最多为 个(称为链接容量)相邻 cell 连接起来。 -
如果在预训练阶段(如逻辑综合阶段)处理问题,将不会有 cell 之间的几何边,并在表示学习阶段设置
,表明 Circuit Graph 与逻辑综合阶段的 circuit 兼容。
将电路设计转化为 Cuircuit Graph 的时间为
Circuit GNN
Overview
Circuit GNN 框架如图 4:
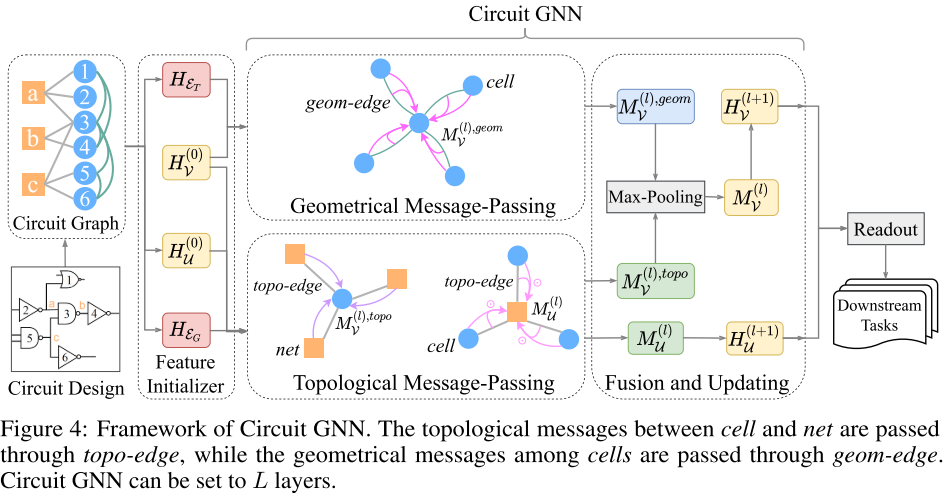
框架首先输入 Circuit Graph
Topo-Geom Message-passing
在
$$
M_{\mathcal{V}}{(l),topo}=\Phi_{msg}{\mathcal{U}\xrightarrow{\varepsilon_{T}}\mathcal{V}}(\mathcal{U},\mathcal{E}{T},\boldsymbol{H}{\mathcal{U}}^{(l)},\boldsymbol{H}{\mathcal{E}{T}})\quad M_{\mathcal{U}}{(l)}=\Phi_{msg}{\mathcal{V}\xrightarrow{\varepsilon_{T}}\mathcal{U}}(\mathcal{V},\mathcal{E}{T},\boldsymbol{H}{\mathcal{V}}^{(l)},\boldsymbol{H}{\mathcal{E}{T}})
$$
-
其中
是当前层数, 是消息函数,用于收集来自 net 发 送 到 ( 类 似 在几何消息传递中,考虑 geom-edges(几何边)
$$
M_{\mathcal{V}}{(l),geom}=\Phi_{msg}{\mathcal{V}\xrightarrow{\varepsilon_{G}}\mathcal{V}}(\mathcal{V},\mathcal{E}{G},\boldsymbol{H}{\mathcal{V}}^{(l)},\boldsymbol{H}{\mathcal{E}{G}})
$$
然后,融合拓扑和几何消息并更新表示:
$$
M_{\mathcal{V}}{(l)}=\mathrm{MaxPooling}(\boldsymbol{M}_{\mathcal{V}}{(l),geom},\boldsymbol{M}{\mathcal{V}}{(l),topo})\boldsymbol{H}_{\mathcal{V}}{(l+1)}=\Phi{update}(\boldsymbol{H}{\mathcal{V}}{(l)},\boldsymbol{M}_{\mathcal{V}}{(l)})\quad\boldsymbol{H}{\mathcal{U}}{(l+1)}=\Phi_{update}(\boldsymbol{H}_{\mathcal{U}}{(l)},\boldsymbol{M}_{\mathcal{U}}^{(l)})
$$
-
其中更新函数为
在设计具体的消息函数
和 中 拓 扑 编 码 和 几 何 信 息 。 在 拓 扑 消 息 传 递 中 , 对 于 , 融 合 周 围
$$
\Phi_{msg}{\mathcal{V}\xrightarrow{\mathcal{E}_{T}}\mathcal{U}}({(\boldsymbol{h}_{v}{\mathcal{V}},\boldsymbol{h}{(v,u)}{\mathcal{E}_{T}})|(v,u)\in\mathcal{E}_{T}})=\sum_{(v,u)\in\mathcal{E}_{T}}(\boldsymbol{W}_{\mathcal{E}_{T}\to\mathcal{U}}\boldsymbol{h}_{(v,u)}{\mathcal{E}{T}})\odot(\boldsymbol{W}{\mathcal{V}\to\mathcal{U}}\boldsymbol{h}{v}^{\mathcal{V}})
$$
-
其中
是 可 学 习 的 权 重 举 证 , 是 元 素 级 相 乘 操 作 。 由 于 表 示 已 经 在 中 收 集 , 在 传 回 的 消 息 中 只 考 虑 表 示
$$
\Phi_{msg}{\mathcal{U}\xrightarrow{\varepsilon_T}\mathcal{V}}({\boldsymbol{h}_u{\mathcal{U}}|(v,u)\in\mathcal{E}T})=\sum{(v,u)\in\mathcal{E}T}\boldsymbol{W}{\mathcal{U}\to\mathcal{V}}\boldsymbol{h}_u^{\mathcal{U}}
$$
在几何消息传递中,为了增强几何信息,在对 cells 进行卷积时候,使用 geom-edges 表示来计算边权重:
$$
\Phi_{msg}{\mathcal{V}\xrightarrow{\mathcal{E}_{G}}\mathcal{V}}({(\boldsymbol{h}_{v{}}{\mathcal{V}},\boldsymbol{h}_{(v,v{})}{\mathcal{E}_{G}})|(v,v{*})\in\mathcal{E}{G}})=\sum{(w,w{*})\subset\mathcal{E}_{-}}(\boldsymbol{a}{\top}\boldsymbol{h}{(v,v{*})}{\mathcal{E}{G}})\cdot\boldsymbol{W}{\mathcal{V}\to\mathcal{V}}\boldsymbol{h}{v{*}}{\mathcal{V}}
$$
-
其中
Discussion of Inference Time
假设 cell,net,topo-edge,gemo-edge 的隐藏层维度分别为 $F_{\mathcal{V}},F_{\mathcal{U}},F_{\mathcal{E}{T}},F{\mathcal{E}{G}}
Task-adaptive Readout
经过
$$
\hat{\boldsymbol{y}}{\mathrm{cell}}=\mathrm{MLP}(\boldsymbol{H}{\mathcal{V}}{(L)}\oplus\boldsymbol{X}_{\mathcal{V}})\quad\hat{\boldsymbol{y}}_{\mathrm{net}}=\mathrm{MLP}(\boldsymbol{H}_{\mathcal{U}}{(L)}\oplus\boldsymbol{X}_{\mathcal{U}})
$$
然而,grid-level(e.g. 芯片图中每个 grid 拥塞预测)将目标分配到每个网咯上,此模型对此不太了解。为了使模型能够在这些任务上训练和评估,通过对 grid 内 cell 表示进行均值池化(mean-pooling)来生成每个网格的输出表示:
$$
\hat{\boldsymbol{y}}\mathrm{grid}=\mathrm{MLP}(\hat{\boldsymbol{M}}\boldsymbol{H}{\mathcal{V}}^{(L)})
$$
-
其中
Experiments
Tasks and Datasets
Congestion Prediction
拥塞预测是在详细布线阶段布线之前预测布线拥塞的任务,被广泛用于布局工具中,提供布局质量的快速反馈,避免较差的布局方案。
本文实验在 12 个 VLSI 设计 ISPD2011 上实验,其中 1/2/3/5/6/7/9/11/14/16 用作训练 training,18 用作评估 validation,19 用作测试 testing。
使用 DREAMPlace 来放置 cells,并初始化 cells,nets,grids 的原始特征。NCTU-GR 2.0 是一种流行的全局布线器(GR),用于生成网格上的拥塞。每个 cell 的拥塞目标设为其所在 grid 的值。对于逻辑综合阶段的拥塞预测,只是用电路的拓扑,几何无关的特征。对于布局阶段的预测,额外使用 DREAMPlace 生成 cell 位置。
在 cell-level 和 grid-level 上用 Pearson/Spearman/Kendall 相关性来比较预测结果和实际结果。还将拥塞值划分为
Net Wirelength Prediction
目标是每个 net 的线长,使用半周线长(HPWL)作为估计。在 DAC2012 上实验,其中 3/6/7/9/11/12/14 用作训练 training,16 用做评估 validation,19 用作测试 testing。DREAMPlace 为每个 net 生成目标。这两阶段的电路特征跟前面提到的拥塞预测相同。
线长回归目标范围从 0~25k,取对数使目标更加平滑。本文评估 Pearson/Spearman/Kendall 相关结果,以及以及平均绝对误差 (MAE) 和均方根误差 (RMSE) 。
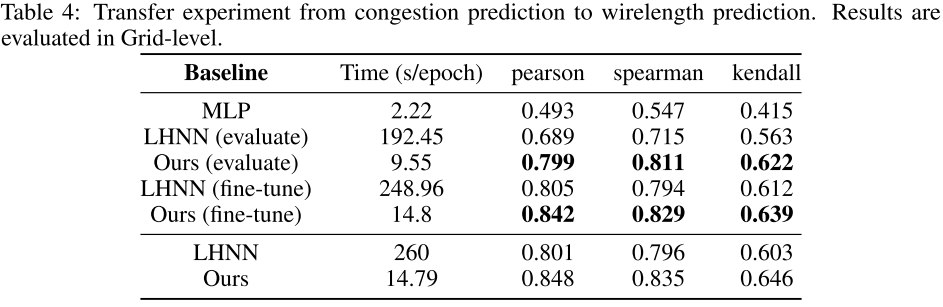
Transfer Task
Transfer 任务是为了进一步评估提取 GNN 特征的代表性。本文首先用拥塞预测任务训练 GNN/LHNN,然后评估/微调它们进行线长预测。
Baselines and Settings
执行上述两项任务,将本文模型跟下面 base 模型相对比。传统 ML method 包括 MLP,图表示模型包括 GCN/GAT/GraphSAGE/MPNN/pix2pix(pix2pix 为 cv 中图像转换模型)。还对 EDA 定制 ML 模型进行实验:
-
CongestionNet:一种用于预测电路的多层注意结构;
-
Net2f/Net2a:使用定制 GNN 的预布局网络表示模型;
-
LHNN:一种提供拓扑信息的几何拥塞预测方法。
为了进一步验证本文模型融合拓扑和几何信息能力,测试了两种变体:
-
Ours (w/o. geom.) :去掉所有几何边;
-
Ours (w/o. topo.) :去掉 def3 中所有拓扑边。
Result of Congestion Prediction
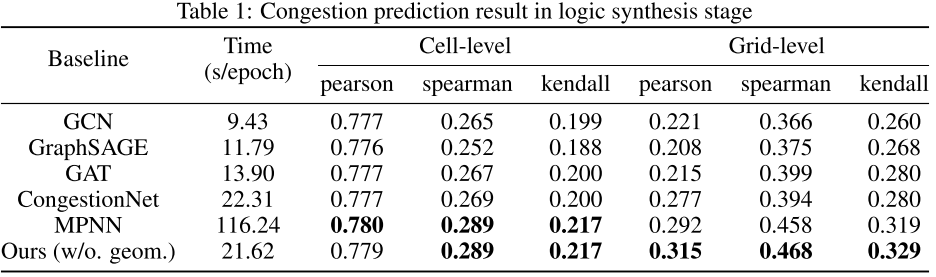
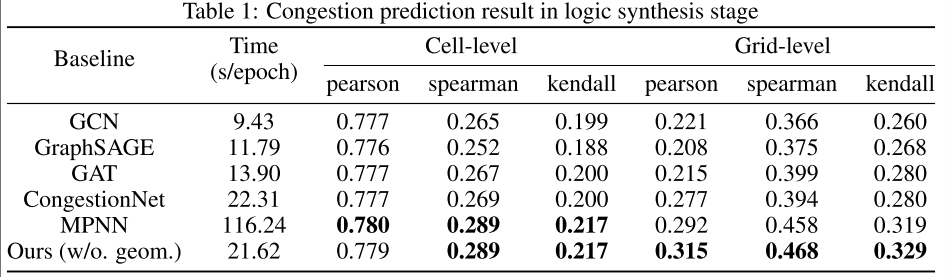
本文在没有几何信息情况下对逻辑综合阶段电路预测结果评估,见表 1:
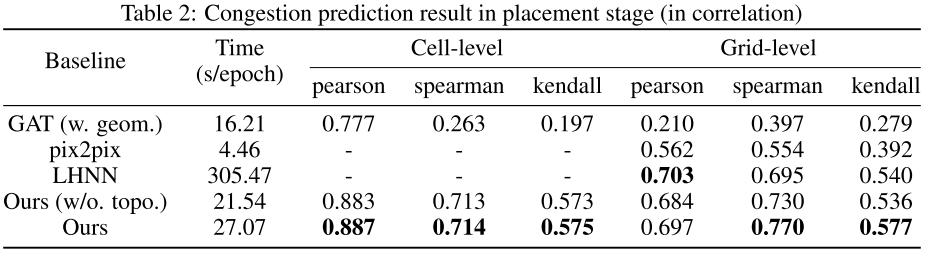
在布局阶段执行相同任务,见表 2 和附表 12:
结果表明:
-
在逻辑综合阶段,对比传统 GNN 模型,仅使用 topo-edges(拓扑边)方法取得了最好的性能(比 CongestionNet 提高 16.7%),并且与传统 GNN 模型相比,时间成本相当于 MPNN。
-
在布局阶段,本文方法在大多数指标上优于最新的 LHNN(平均 5.6%),而运行时间只有 LHNN 的十分之一。模型卓越性能主要归功于拓扑信息和几何信息的融合。
图 5 展示了不同方法可视化预测值。可以看出本文方法生成更精细的拥塞预测,并且具有更好的区分性。

Result of Net Wirelength Prediction
Net 线长预测结果如附表 11(逻辑综合阶段)、表 3 和图 6(布局阶段所示)。通过读出 LHNN 在中间阶段生成的 net 来获得该任务结果。
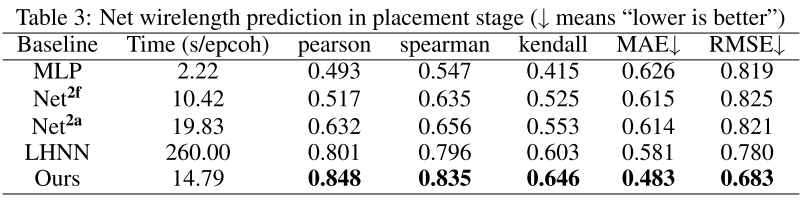
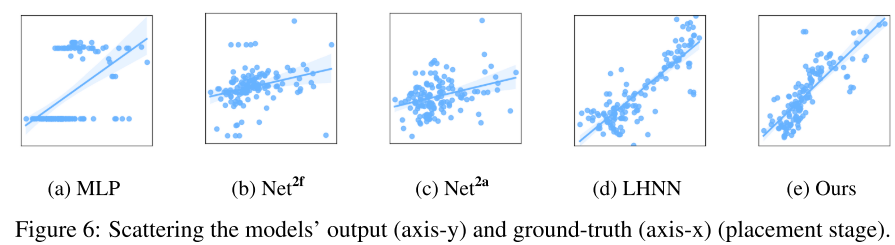
结果表明,该模型达到了 SOTA 性能,并且在时间成本上与 Net2 和 Net2a 媲美。
Result of Transfer Task
实验设置:
-
对于评估(evaluation)设置,重新从头训练一个不同的读出模块,但 GNN 的参数保持不变。
-
对于微调(fine-tuning)设置,重新从头训练一个不同的读出模块,同时微调 GNN 的参数。
-
对于评估和微调(evaluation & fine-tuning),LHNN 和我们的模型仅在默认设置的 1/5 轮次上进行训练,以展示所学特征的可迁移性
表 4 给出了结果,表明电路 GNN 从拥塞预测中学习到的只是很容易迁移到另一个任务上(无论是直接使用还是微调),而 LHNN 的可移植性较弱。